Conteo geométrico de triángulos en el techo del Movistar Arena
Published:
La arquitectura contemporánea ofrece múltiples ejemplos en los que el diseño geométrico trasciende su función estructural o estética y se convierte en una oportunidad para el análisis matemático. El techo del Movistar Arena constituye un caso particularmente sugerente, al presentar un patrón regular de subdivisiones triangulares que invita a reflexionar sobre simetría, repetición y conteo geométrico.
La reflexión que se presenta a continuación surge a partir de la observación directa de este patrón, con el objetivo de responder una pregunta concreta: ¿cuántos triángulos pequeños componen la totalidad del diseño del techo?
Para abordar el problema, resulta conveniente comenzar desde el centro del patrón. En el primer grupo identificable se observan ocho triángulos básicos, los cuales constituyen la unidad inicial de repetición del diseño.
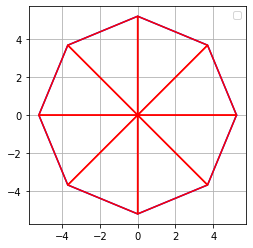
Figura 1: Grupo central inicial, compuesto por ocho triángulos.
Al extender el análisis hacia el siguiente nivel, se observa que cada triángulo del grupo anterior se subdivide en cuatro triángulos: uno central y tres adicionales. En consecuencia, el número total de triángulos en este segundo nivel corresponde a 8 × 4 = 32.
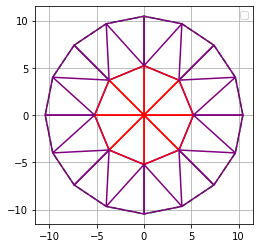
Figura 2: Segundo nivel del patrón, con cuatro triángulos por unidad inicial.
El patrón de crecimiento continúa de manera regular. En el siguiente grupo, cada unidad pasa a contener nueve triángulos, lo que conduce a un total de 8 × 9 = 72 triángulos en ese nivel.
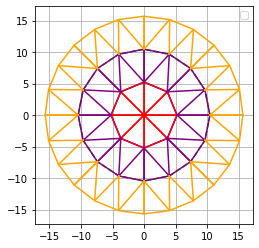
Figura 3: Tercer nivel del patrón, con nueve triángulos por unidad inicial.
Este esquema de crecimiento se repite de forma consistente a lo largo del diseño completo. Al contabilizar un total de 18 grupos equivalentes, el número total de triángulos pequeños presentes en el techo puede calcularse como:
8 × 18 × 18 = 2592
Este ejercicio ilustra cómo un elemento arquitectónico cotidiano puede convertirse en un objeto de análisis matemático, permitiendo vincular observación espacial, reconocimiento de patrones y razonamiento cuantitativo en un contexto no académico, pero conceptualmente riguroso.