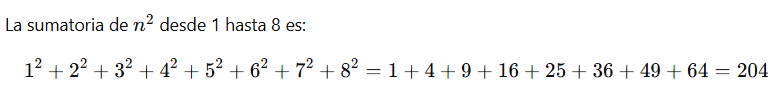¿Cuántos cuadrados hay en un tablero de ajedrez? Un problema clásico de conteo geométrico
Published:
El problema de determinar cuántos cuadrados existen en un tablero de ajedrez es un ejercicio clásico de la geometría recreativa y de la divulgación matemática. A pesar de su aparente simplicidad, este problema permite ilustrar de forma clara cómo los patrones geométricos y las sumatorias numéricas emergen de una observación sistemática de una estructura bidimensional regular.
Un tablero de ajedrez estándar está compuesto por una cuadrícula de 8 × 8 casillas. La intuición inicial suele llevar a contar únicamente los 64 cuadrados unitarios que conforman la base del tablero. Sin embargo, esta aproximación omite una cantidad significativa de cuadrados de mayor tamaño que se forman al agrupar casillas adyacentes.
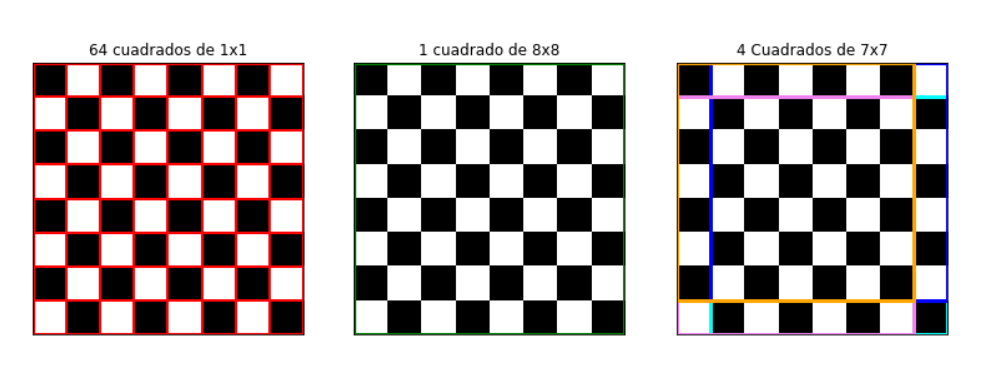
Figura 1: Representación esquemática de los distintos tamaños de cuadrados presentes en una cuadrícula 8 × 8.
Para abordar el conteo completo, es necesario considerar todos los cuadrados posibles de lado n, donde n varía desde 1 hasta 8. Para cada valor de n, el número de cuadrados de lado n que pueden formarse en el tablero corresponde a n².
De este modo, el número total de cuadrados presentes en el tablero se obtiene sumando los cuadrados de los números naturales desde 1 hasta 8:
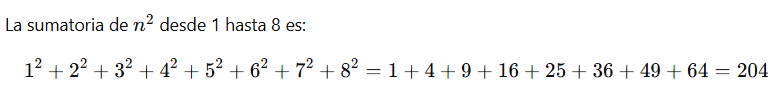
Figura 2: Sumatoria de n² desde 1 hasta 8.
El resultado indica que un tablero de ajedrez contiene un total de 204 cuadrados, considerando todas las posibles escalas. Este tipo de problemas resulta especialmente valioso en contextos educativos, ya que permite conectar visualización geométrica, razonamiento algebraico y pensamiento combinatorio de manera accesible y rigurosa.
Más allá de su carácter recreativo, este ejercicio pone de manifiesto la importancia de analizar una estructura desde múltiples niveles de observación, recordando que muchas configuraciones matemáticas esconden una riqueza mayor a la que sugiere una primera mirada.